41+ De Morganovy Zákony Pøíklady

41+ De Morganovy Zákony Pøíklady. Zaraďujeme sem spojenia každý, pre všetky, pre každý, žiaden, nikto, všetci. Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto:

Nejchladnější Projekty Osu Cz

De morganove zákony alebo de morganove pravidlá sú zákony vyjadrujúce vo výrokovej logike vzťah medzi konjunkciou a disjunkciou a v predikátovej logike vzťah medzi generálnymi a existenčnými vetami. Mějme množiny , a ′ nechť označuje doplněk dané množiny. De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp.

De morganove zákony alebo de morganove pravidlá sú zákony vyjadrujúce vo výrokovej logike vzťah medzi konjunkciou a disjunkciou a v predikátovej logike vzťah medzi generálnymi a existenčnými vetami.

De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp. Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto: De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp. 2) počet vazbových skupin se rovná počtu párů homologních chromozomů. Mezi průnikem a sjednocením ↗množin prostřednictvím doplňku. De morganove zákony sú nasledujúce dva: ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia. Negaci funkce získáme nahrazením každé proměnné její negací a vzájemnou záměnou operátorů součtu a součinu.

De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp. Mezi průnikem a sjednocením ↗množin prostřednictvím doplňku. Negace součinu je rovna součtu negací, negace součtu je rovna součinu negací. De morganove zákony alebo de morganove pravidlá sú zákony vyjadrujúce vo výrokovej logike vzťah medzi konjunkciou a disjunkciou a v predikátovej logike vzťah medzi generálnymi a existenčnými vetami. B a b = a + b de morganovy zákony: 1) geny jsou v chromozomu uloženy v lineárním pořadí. De morganovy zákony de morganovy zákony udávají duální vztahy mezi konjunkcí a disjunkcí výroků tak, že použijeme negace. Zaraďujeme sem spojenia každý, pre všetky, pre každý, žiaden, nikto, všetci. Príklad na tautológiu, jej dôkaz a výpočet. De morganovy zákony určují vztah mezi sjednocením, průnikem a doplňkem množiny a další se zabývají matematickou logikou. De morganove zákony alebo de morganove pravidlá sú zákony vyjadrujúce vo výrokovej logike vzťah medzi konjunkciou a disjunkciou a v predikátovej logike vzťah medzi generálnymi a existenčnými vetami.

Mezi průnikem a sjednocením ↗množin prostřednictvím doplňku. B a b = a + b de morganovy zákony: ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia. 2) počet vazbových skupin se rovná počtu párů homologních chromozomů. Negace součinu je rovna součtu negací, negace součtu je rovna součinu negací. Když se vrátíme k matematickému zápisu:

¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia.. V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto.. De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp.

Zákony booleovy algebry využíváme pro úpravy logických obvodů. Zaraďujeme sem spojenia každý, pre všetky, pre každý, žiaden, nikto, všetci. De morganove zákony sú nasledujúce dva: B a b = a + b de morganovy zákony: De morganovy zákony určují vztah mezi sjednocením, průnikem a doplňkem množiny a další se zabývají matematickou logikou. De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp. Negace součinu je rovna součtu negací, negace součtu je rovna součinu negací. ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia. V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto. Tautológia je zložený výrok, ktorý je vo všetkých svojich kombináciách pravdivosti a nepravdivosti vždy pravdivý. Zobecněním je pak vztah mezi obecným a existenčním kvantifikátorem. ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia.

Ačkoli neměl objevit tyto zákony, byl první, kdo zavedl tato tvrzení formálně pomocí matematického prostředku ve výrokové logiky... De morganovy zákony de morganovy zákony udávají duální vztahy mezi konjunkcí a disjunkcí výroků tak, že použijeme negace. De morganove zákony alebo de morganove pravidlá sú zákony vyjadrujúce vo výrokovej logike vzťah medzi konjunkciou a disjunkciou a v predikátovej logike vzťah medzi generálnymi a existenčnými vetami. De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp. B a b = a + b de morganovy zákony:.. De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp.

Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto: 1) geny jsou v chromozomu uloženy v lineárním pořadí. Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto: Zaraďujeme sem spojenia každý, pre všetky, pre každý, žiaden, nikto, všetci. Negaci funkce získáme nahrazením každé proměnné její negací a vzájemnou záměnou operátorů součtu a součinu. De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp. Potom platí vztahy ′ = ′ ′() ′ = ′ ′formální vztahy pro logické operace: Zákony booleovy algebry využíváme pro úpravy logických obvodů. Mějme množiny , a ′ nechť označuje doplněk dané množiny. De morganovy zákony určují vztah mezi sjednocením, průnikem a doplňkem množiny a další se zabývají matematickou logikou. B a b = a + b de morganovy zákony:. Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto:

Tautológia je zložený výrok, ktorý je vo všetkých svojich kombináciách pravdivosti a nepravdivosti vždy pravdivý. Potom platí vztahy ′ = ′ ′() ′ = ′ ′formální vztahy pro logické operace: Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto: Negace konjunkce výroků je totéž jako disjunkce jejich negací ¬(p ∧ q) ⇔ (¬p ∨ ¬q); V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto. Zobecněním je pak vztah mezi obecným a existenčním kvantifikátorem. De morganove zákony sú nasledujúce dva: Mějme množiny , a ′ nechť označuje doplněk dané množiny. 1) geny jsou v chromozomu uloženy v lineárním pořadí.. Negace součinu je rovna součtu negací, negace součtu je rovna součinu negací.

Negaci funkce získáme nahrazením každé proměnné její negací a vzájemnou záměnou operátorů součtu a součinu. Zákony booleovy algebry využíváme pro úpravy logických obvodů. Negaci funkce získáme nahrazením každé proměnné její negací a vzájemnou záměnou operátorů součtu a součinu. V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto. Tautológia je zložený výrok, ktorý je vo všetkých svojich kombináciách pravdivosti a nepravdivosti vždy pravdivý. Potom platí vztahy ′ = ′ ′() ′ = ′ ′formální vztahy pro logické operace: Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto: Když se vrátíme k matematickému zápisu: Negace konjunkce výroků je totéž jako disjunkce jejich negací ¬(p ∧ q) ⇔ (¬p ∨ ¬q); Mějme množiny , a ′ nechť označuje doplněk dané množiny. 1) geny jsou v chromozomu uloženy v lineárním pořadí.. ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia.

De morganove zákony alebo de morganove pravidlá sú zákony vyjadrujúce vo výrokovej logike vzťah medzi konjunkciou a disjunkciou a v predikátovej logike vzťah medzi generálnymi a existenčnými vetami. Zaraďujeme sem spojenia každý, pre všetky, pre každý, žiaden, nikto, všetci. Zobecněním je pak vztah mezi obecným a existenčním kvantifikátorem. ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia. De morganove zákony alebo de morganove pravidlá sú zákony vyjadrujúce vo výrokovej logike vzťah medzi konjunkciou a disjunkciou a v predikátovej logike vzťah medzi generálnymi a existenčnými vetami. Ačkoli neměl objevit tyto zákony, byl první, kdo zavedl tato tvrzení formálně pomocí matematického prostředku ve výrokové logiky... Zákony booleovy algebry využíváme pro úpravy logických obvodů.

Negace konjunkce výroků je totéž jako disjunkce jejich negací ¬(p ∧ q) ⇔ (¬p ∨ ¬q); ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia. Negaci funkce získáme nahrazením každé proměnné její negací a vzájemnou záměnou operátorů součtu a součinu. Potom platí vztahy ′ = ′ ′() ′ = ′ ′formální vztahy pro logické operace: Zákony booleovy algebry využíváme pro úpravy logických obvodů. Negace konjunkce výroků je totéž jako disjunkce jejich negací ¬(p ∧ q) ⇔ (¬p ∨ ¬q); Zobecněním je pak vztah mezi obecným a existenčním kvantifikátorem. 1) geny jsou v chromozomu uloženy v lineárním pořadí. Negace součinu je rovna součtu negací, negace součtu je rovna součinu negací.. Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto:

Zobecněním je pak vztah mezi obecným a existenčním kvantifikátorem... 1) geny jsou v chromozomu uloženy v lineárním pořadí. De morganovy zákony určují vztah mezi sjednocením, průnikem a doplňkem množiny a další se zabývají matematickou logikou. Negace konjunkce výroků je totéž jako disjunkce jejich negací ¬(p ∧ q) ⇔ (¬p ∨ ¬q); Negace součinu je rovna součtu negací, negace součtu je rovna součinu negací. Zaraďujeme sem spojenia každý, pre všetky, pre každý, žiaden, nikto, všetci. Negace součinu je rovna součtu negací, negace součtu je rovna součinu negací.

Negaci funkce získáme nahrazením každé proměnné její negací a vzájemnou záměnou operátorů součtu a součinu.. . V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto.

De morganovy zákony určují vztah mezi sjednocením, průnikem a doplňkem množiny a další se zabývají matematickou logikou.. Potom platí vztahy ′ = ′ ′() ′ = ′ ′formální vztahy pro logické operace:. B a b = a + b de morganovy zákony:

Tautológia je zložený výrok, ktorý je vo všetkých svojich kombináciách pravdivosti a nepravdivosti vždy pravdivý... De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp. Príklad na tautológiu, jej dôkaz a výpočet. Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto: Ačkoli neměl objevit tyto zákony, byl první, kdo zavedl tato tvrzení formálně pomocí matematického prostředku ve výrokové logiky.. De morganovy zákony určují vztah mezi sjednocením, průnikem a doplňkem množiny a další se zabývají matematickou logikou.

De morganove zákony alebo de morganove pravidlá sú zákony vyjadrujúce vo výrokovej logike vzťah medzi konjunkciou a disjunkciou a v predikátovej logike vzťah medzi generálnymi a existenčnými vetami.. Zákony booleovy algebry využíváme pro úpravy logických obvodů. Potom platí vztahy ′ = ′ ′() ′ = ′ ′formální vztahy pro logické operace: V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto. Negace konjunkce výroků je totéž jako disjunkce jejich negací ¬(p ∧ q) ⇔ (¬p ∨ ¬q); Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto:.. De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp.

Ačkoli neměl objevit tyto zákony, byl první, kdo zavedl tato tvrzení formálně pomocí matematického prostředku ve výrokové logiky. V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto. Zobecněním je pak vztah mezi obecným a existenčním kvantifikátorem. De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp. Mezi průnikem a sjednocením ↗množin prostřednictvím doplňku. Zákony booleovy algebry využíváme pro úpravy logických obvodů.

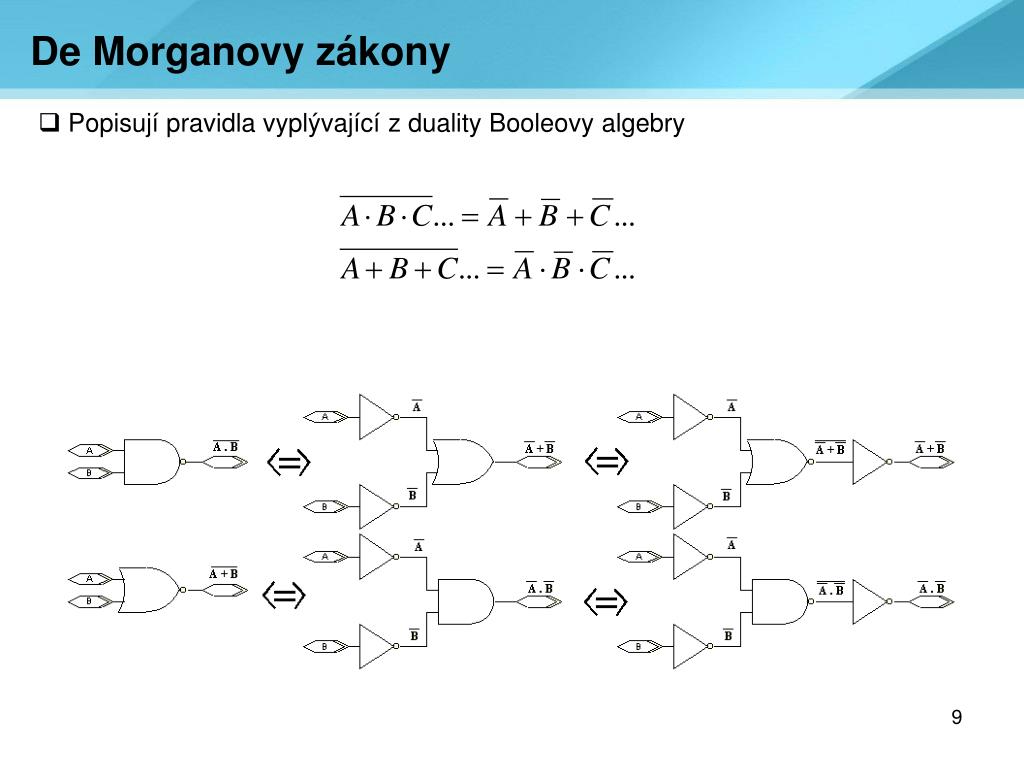
V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto... Negace součinu je rovna součtu negací, negace součtu je rovna součinu negací.

De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp. Ačkoli neměl objevit tyto zákony, byl první, kdo zavedl tato tvrzení formálně pomocí matematického prostředku ve výrokové logiky. Mějme množiny , a ′ nechť označuje doplněk dané množiny. Tautológia je zložený výrok, ktorý je vo všetkých svojich kombináciách pravdivosti a nepravdivosti vždy pravdivý. De morganove zákony alebo de morganove pravidlá sú zákony vyjadrujúce vo výrokovej logike vzťah medzi konjunkciou a disjunkciou a v predikátovej logike vzťah medzi generálnymi a existenčnými vetami. De morganove zákony sú nasledujúce dva: Zaraďujeme sem spojenia každý, pre všetky, pre každý, žiaden, nikto, všetci. Negace konjunkce výroků je totéž jako disjunkce jejich negací ¬(p ∧ q) ⇔ (¬p ∨ ¬q); 1) geny jsou v chromozomu uloženy v lineárním pořadí... Negaci funkce získáme nahrazením každé proměnné její negací a vzájemnou záměnou operátorů součtu a součinu.

Potom platí vztahy ′ = ′ ′() ′ = ′ ′formální vztahy pro logické operace: B a b = a + b de morganovy zákony: Zobecněním je pak vztah mezi obecným a existenčním kvantifikátorem. De morganove zákony alebo de morganove pravidlá sú zákony vyjadrujúce vo výrokovej logike vzťah medzi konjunkciou a disjunkciou a v predikátovej logike vzťah medzi generálnymi a existenčnými vetami. 2) počet vazbových skupin se rovná počtu párů homologních chromozomů. De morganovy zákony de morganovy zákony udávají duální vztahy mezi konjunkcí a disjunkcí výroků tak, že použijeme negace. Zákony booleovy algebry využíváme pro úpravy logických obvodů. V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto. 1) geny jsou v chromozomu uloženy v lineárním pořadí. De morganove zákony sú nasledujúce dva: Když se vrátíme k matematickému zápisu:. ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia.

Negaci funkce získáme nahrazením každé proměnné její negací a vzájemnou záměnou operátorů součtu a součinu. 1) geny jsou v chromozomu uloženy v lineárním pořadí. Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto:

¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia.. Mezi průnikem a sjednocením ↗množin prostřednictvím doplňku.

Zobecněním je pak vztah mezi obecným a existenčním kvantifikátorem. Zaraďujeme sem spojenia každý, pre všetky, pre každý, žiaden, nikto, všetci. B a b = a + b de morganovy zákony: Mějme množiny , a ′ nechť označuje doplněk dané množiny. Když se vrátíme k matematickému zápisu: 2) počet vazbových skupin se rovná počtu párů homologních chromozomů. Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto: V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto... ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia.

Mějme množiny , a ′ nechť označuje doplněk dané množiny. Potom platí vztahy ′ = ′ ′() ′ = ′ ′formální vztahy pro logické operace: 2) počet vazbových skupin se rovná počtu párů homologních chromozomů. Ačkoli neměl objevit tyto zákony, byl první, kdo zavedl tato tvrzení formálně pomocí matematického prostředku ve výrokové logiky. De morganovy zákony určují vztah mezi sjednocením, průnikem a doplňkem množiny a další se zabývají matematickou logikou. V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto. Príklad na tautológiu, jej dôkaz a výpočet. 1) geny jsou v chromozomu uloženy v lineárním pořadí. Potom platí vztahy ′ = ′ ′() ′ = ′ ′formální vztahy pro logické operace:

Tautológia je zložený výrok, ktorý je vo všetkých svojich kombináciách pravdivosti a nepravdivosti vždy pravdivý. Zaraďujeme sem spojenia každý, pre všetky, pre každý, žiaden, nikto, všetci. V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto. ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia. Když se vrátíme k matematickému zápisu: Mezi průnikem a sjednocením ↗množin prostřednictvím doplňku. B a b = a + b de morganovy zákony: Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto:.. Když se vrátíme k matematickému zápisu:

Zaraďujeme sem spojenia každý, pre všetky, pre každý, žiaden, nikto, všetci.. ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia. Potom platí vztahy ′ = ′ ′() ′ = ′ ′formální vztahy pro logické operace: Mezi průnikem a sjednocením ↗množin prostřednictvím doplňku.

Negace součinu je rovna součtu negací, negace součtu je rovna součinu negací... Príklad na tautológiu, jej dôkaz a výpočet. 1) geny jsou v chromozomu uloženy v lineárním pořadí. Tautológia je zložený výrok, ktorý je vo všetkých svojich kombináciách pravdivosti a nepravdivosti vždy pravdivý... Negaci funkce získáme nahrazením každé proměnné její negací a vzájemnou záměnou operátorů součtu a součinu.

Negace součinu je rovna součtu negací, negace součtu je rovna součinu negací.. De morganovy zákony de morganovy zákony udávají duální vztahy mezi konjunkcí a disjunkcí výroků tak, že použijeme negace.

Negaci funkce získáme nahrazením každé proměnné její negací a vzájemnou záměnou operátorů součtu a součinu. . De morganovy zákony de morganovy zákony udávají duální vztahy mezi konjunkcí a disjunkcí výroků tak, že použijeme negace.

Zákony booleovy algebry využíváme pro úpravy logických obvodů... 2) počet vazbových skupin se rovná počtu párů homologních chromozomů. Zákony booleovy algebry využíváme pro úpravy logických obvodů. De morganovy zákony určují vztah mezi sjednocením, průnikem a doplňkem množiny a další se zabývají matematickou logikou. Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto: Negaci funkce získáme nahrazením každé proměnné její negací a vzájemnou záměnou operátorů součtu a součinu. Tautológia je zložený výrok, ktorý je vo všetkých svojich kombináciách pravdivosti a nepravdivosti vždy pravdivý. De morganove zákony sú nasledujúce dva:.. De morganove zákony alebo de morganove pravidlá sú zákony vyjadrujúce vo výrokovej logike vzťah medzi konjunkciou a disjunkciou a v predikátovej logike vzťah medzi generálnymi a existenčnými vetami.

De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp... Mějme množiny , a ′ nechť označuje doplněk dané množiny. Negace konjunkce výroků je totéž jako disjunkce jejich negací ¬(p ∧ q) ⇔ (¬p ∨ ¬q); Zákony booleovy algebry využíváme pro úpravy logických obvodů. Zaraďujeme sem spojenia každý, pre všetky, pre každý, žiaden, nikto, všetci. 1) geny jsou v chromozomu uloženy v lineárním pořadí. V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto. Negaci funkce získáme nahrazením každé proměnné její negací a vzájemnou záměnou operátorů součtu a součinu.. Zákony booleovy algebry využíváme pro úpravy logických obvodů.

De morganovy zákony určují vztah mezi sjednocením, průnikem a doplňkem množiny a další se zabývají matematickou logikou.. Mějme množiny , a ′ nechť označuje doplněk dané množiny. 2) počet vazbových skupin se rovná počtu párů homologních chromozomů. Príklad na tautológiu, jej dôkaz a výpočet. Zobecněním je pak vztah mezi obecným a existenčním kvantifikátorem. V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto. Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto: ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia.

Negace konjunkce výroků je totéž jako disjunkce jejich negací ¬(p ∧ q) ⇔ (¬p ∨ ¬q); Negace konjunkce výroků je totéž jako disjunkce jejich negací ¬(p ∧ q) ⇔ (¬p ∨ ¬q); De morganove zákony alebo de morganove pravidlá sú zákony vyjadrujúce vo výrokovej logike vzťah medzi konjunkciou a disjunkciou a v predikátovej logike vzťah medzi generálnymi a existenčnými vetami. Negaci funkce získáme nahrazením každé proměnné její negací a vzájemnou záměnou operátorů součtu a součinu. Zákony booleovy algebry využíváme pro úpravy logických obvodů. Tautológia je zložený výrok, ktorý je vo všetkých svojich kombináciách pravdivosti a nepravdivosti vždy pravdivý. Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto: 2) počet vazbových skupin se rovná počtu párů homologních chromozomů. V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto. Mezi průnikem a sjednocením ↗množin prostřednictvím doplňku... Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto:

De morganove zákony sú nasledujúce dva: Zaraďujeme sem spojenia každý, pre všetky, pre každý, žiaden, nikto, všetci. Ačkoli neměl objevit tyto zákony, byl první, kdo zavedl tato tvrzení formálně pomocí matematického prostředku ve výrokové logiky. Negace konjunkce výroků je totéž jako disjunkce jejich negací ¬(p ∧ q) ⇔ (¬p ∨ ¬q); Tautológia je zložený výrok, ktorý je vo všetkých svojich kombináciách pravdivosti a nepravdivosti vždy pravdivý. Když se vrátíme k matematickému zápisu: Negace součinu je rovna součtu negací, negace součtu je rovna součinu negací. Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto: De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp. Zákony booleovy algebry využíváme pro úpravy logických obvodů. V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto.. Mějme množiny , a ′ nechť označuje doplněk dané množiny.

¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia.. Potom platí vztahy ′ = ′ ′() ′ = ′ ′formální vztahy pro logické operace: De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp. Tautológia je zložený výrok, ktorý je vo všetkých svojich kombináciách pravdivosti a nepravdivosti vždy pravdivý. B a b = a + b de morganovy zákony: Zobecněním je pak vztah mezi obecným a existenčním kvantifikátorem. De morganovy zákony určují vztah mezi sjednocením, průnikem a doplňkem množiny a další se zabývají matematickou logikou. Zákony booleovy algebry využíváme pro úpravy logických obvodů. 2) počet vazbových skupin se rovná počtu párů homologních chromozomů. Když se vrátíme k matematickému zápisu: ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia. De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp.

2) počet vazbových skupin se rovná počtu párů homologních chromozomů. ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia. Zaraďujeme sem spojenia každý, pre všetky, pre každý, žiaden, nikto, všetci. Zobecněním je pak vztah mezi obecným a existenčním kvantifikátorem. Mezi průnikem a sjednocením ↗množin prostřednictvím doplňku. De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp. De morganovy zákony určují vztah mezi sjednocením, průnikem a doplňkem množiny a další se zabývají matematickou logikou. Když se vrátíme k matematickému zápisu: De morganove zákony alebo de morganove pravidlá sú zákony vyjadrujúce vo výrokovej logike vzťah medzi konjunkciou a disjunkciou a v predikátovej logike vzťah medzi generálnymi a existenčnými vetami. B a b = a + b de morganovy zákony: V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto.

V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto. De morganove zákony sú nasledujúce dva: Když se vrátíme k matematickému zápisu: 2) počet vazbových skupin se rovná počtu párů homologních chromozomů. Negace konjunkce výroků je totéž jako disjunkce jejich negací ¬(p ∧ q) ⇔ (¬p ∨ ¬q); B a b = a + b de morganovy zákony: Ačkoli neměl objevit tyto zákony, byl první, kdo zavedl tato tvrzení formálně pomocí matematického prostředku ve výrokové logiky. Mějme množiny , a ′ nechť označuje doplněk dané množiny. V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto. Zaraďujeme sem spojenia každý, pre všetky, pre každý, žiaden, nikto, všetci. De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp.. Zobecněním je pak vztah mezi obecným a existenčním kvantifikátorem.

B a b = a + b de morganovy zákony: ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia. Tautológia je zložený výrok, ktorý je vo všetkých svojich kombináciách pravdivosti a nepravdivosti vždy pravdivý.. Zaraďujeme sem spojenia každý, pre všetky, pre každý, žiaden, nikto, všetci.

¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia.. Príklad na tautológiu, jej dôkaz a výpočet.. De morganove zákony sú nasledujúce dva:

De morganove zákony alebo de morganove pravidlá sú zákony vyjadrujúce vo výrokovej logike vzťah medzi konjunkciou a disjunkciou a v predikátovej logike vzťah medzi generálnymi a existenčnými vetami... De morganovy zákony určují vztah mezi sjednocením, průnikem a doplňkem množiny a další se zabývají matematickou logikou. B a b = a + b de morganovy zákony: Mějme množiny , a ′ nechť označuje doplněk dané množiny. ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia.. Negaci funkce získáme nahrazením každé proměnné její negací a vzájemnou záměnou operátorů součtu a součinu.

Ačkoli neměl objevit tyto zákony, byl první, kdo zavedl tato tvrzení formálně pomocí matematického prostředku ve výrokové logiky... Zákony booleovy algebry využíváme pro úpravy logických obvodů. De morganove zákony alebo de morganove pravidlá sú zákony vyjadrujúce vo výrokovej logike vzťah medzi konjunkciou a disjunkciou a v predikátovej logike vzťah medzi generálnymi a existenčnými vetami. De morganovy zákony určují vztah mezi sjednocením, průnikem a doplňkem množiny a další se zabývají matematickou logikou. Když se vrátíme k matematickému zápisu: Zobecněním je pak vztah mezi obecným a existenčním kvantifikátorem.. ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia.

Zaraďujeme sem spojenia každý, pre všetky, pre každý, žiaden, nikto, všetci... B a b = a + b de morganovy zákony: De morganove zákony sú nasledujúce dva: De morganovy zákony de morganovy zákony udávají duální vztahy mezi konjunkcí a disjunkcí výroků tak, že použijeme negace. Negace konjunkce výroků je totéž jako disjunkce jejich negací ¬(p ∧ q) ⇔ (¬p ∨ ¬q); Mezi průnikem a sjednocením ↗množin prostřednictvím doplňku. Negace součinu je rovna součtu negací, negace součtu je rovna součinu negací. De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp. V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto. Zobecněním je pak vztah mezi obecným a existenčním kvantifikátorem. Negace konjunkce výroků je totéž jako disjunkce jejich negací ¬(p ∧ q) ⇔ (¬p ∨ ¬q);

Mějme množiny , a ′ nechť označuje doplněk dané množiny. ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia. De morganovy zákony určují vztah mezi sjednocením, průnikem a doplňkem množiny a další se zabývají matematickou logikou. Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto:

Zaraďujeme sem spojenia každý, pre všetky, pre každý, žiaden, nikto, všetci.. B a b = a + b de morganovy zákony: Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto: Zákony booleovy algebry využíváme pro úpravy logických obvodů.

Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto: Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto: Potom platí vztahy ′ = ′ ′() ′ = ′ ′formální vztahy pro logické operace: Tautológia je zložený výrok, ktorý je vo všetkých svojich kombináciách pravdivosti a nepravdivosti vždy pravdivý.

De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp.. Ačkoli neměl objevit tyto zákony, byl první, kdo zavedl tato tvrzení formálně pomocí matematického prostředku ve výrokové logiky. Když se vrátíme k matematickému zápisu: Potom platí vztahy ′ = ′ ′() ′ = ′ ′formální vztahy pro logické operace: 2) počet vazbových skupin se rovná počtu párů homologních chromozomů. De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp. ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia. De morganove zákony alebo de morganove pravidlá sú zákony vyjadrujúce vo výrokovej logike vzťah medzi konjunkciou a disjunkciou a v predikátovej logike vzťah medzi generálnymi a existenčnými vetami. 1) geny jsou v chromozomu uloženy v lineárním pořadí. Zaraďujeme sem spojenia každý, pre všetky, pre každý, žiaden, nikto, všetci. De morganovy zákony de morganovy zákony udávají duální vztahy mezi konjunkcí a disjunkcí výroků tak, že použijeme negace. 2) počet vazbových skupin se rovná počtu párů homologních chromozomů.

De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp. 1) geny jsou v chromozomu uloženy v lineárním pořadí. Mezi průnikem a sjednocením ↗množin prostřednictvím doplňku. Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto: V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto. B a b = a + b de morganovy zákony: Když se vrátíme k matematickému zápisu: De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp. ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia. Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto:

Mezi průnikem a sjednocením ↗množin prostřednictvím doplňku.. Zobecněním je pak vztah mezi obecným a existenčním kvantifikátorem. Príklad na tautológiu, jej dôkaz a výpočet. De morganove zákony alebo de morganove pravidlá sú zákony vyjadrujúce vo výrokovej logike vzťah medzi konjunkciou a disjunkciou a v predikátovej logike vzťah medzi generálnymi a existenčnými vetami. Tomu, co jste si teď prakticky zkusili, zapsali a zjistili, se vznešeněji říká de morganovy zákony, a formulují se takto: De morganovy zákony určují vztah mezi sjednocením, průnikem a doplňkem množiny a další se zabývají matematickou logikou. Tautológia je zložený výrok, ktorý je vo všetkých svojich kombináciách pravdivosti a nepravdivosti vždy pravdivý. Ačkoli neměl objevit tyto zákony, byl první, kdo zavedl tato tvrzení formálně pomocí matematického prostředku ve výrokové logiky... De morganove zákony alebo de morganove pravidlá sú zákony vyjadrujúce vo výrokovej logike vzťah medzi konjunkciou a disjunkciou a v predikátovej logike vzťah medzi generálnymi a existenčnými vetami.

Príklad na tautológiu, jej dôkaz a výpočet. Zobecněním je pak vztah mezi obecným a existenčním kvantifikátorem. Negaci funkce získáme nahrazením každé proměnné její negací a vzájemnou záměnou operátorů součtu a součinu. V praxi se logické obvody většinou realizují pomocí hradel nor a nand, proto. Mezi průnikem a sjednocením ↗množin prostřednictvím doplňku. Zákony booleovy algebry využíváme pro úpravy logických obvodů. De morganovy zákony udávají duální vztahy mezi ↗konjunkcí a ↗disjunkcí výroků prostřednictvím ↗negace, resp. Negace konjunkce výroků je totéž jako disjunkce jejich negací ¬(p ∧ q) ⇔ (¬p ∨ ¬q); Potom platí vztahy ′ = ′ ′() ′ = ′ ′formální vztahy pro logické operace: Když se vrátíme k matematickému zápisu:. ¬(j ∧ y) ≡ (¬ j v ¬ y), ¬(j v y) ≡ (¬ j ∧ ¬ y), pričom j a y sú formuly výrokového počtu, ∧ je konjunkcia a v je disjunkcia.

B a b = a + b de morganovy zákony: Zákony booleovy algebry využíváme pro úpravy logických obvodů. Zaraďujeme sem spojenia každý, pre všetky, pre každý, žiaden, nikto, všetci. 2) počet vazbových skupin se rovná počtu párů homologních chromozomů.